1.论文动机

        近年来，随着深度传感器的逐渐普及，三维深度数据的获取越来越容易。与此同时， VR、AR、扫地机器人、自动驾驶等相关应用的兴起，对物体、场景与人的三维重建与实时三维位置定位等需求也越来越大。为了将不同视角下获取的深度数据进行融合，需基于刚性配准算法将源点云经过刚性变换后与目标点云尽可能匹配。因此，刚性配准算法是三维重建、SLAM等应用的关键核心技术。

        迭代最近点算法(ICP)是刚性配准中最普遍采用的算法，该方法在寻找对应关系与更新刚性变换之间交替迭代，直至收敛。然而，现有ICP算法普遍采用二范数来衡量配准误差，这导致现有方法易受异常值与缺失数据的影响。另外，在采用该方法进行交替迭代时算法收敛速度较慢。因此，现有ICP方法仍然存在精度与速度这两方面的问题。

        针对以上问题，中国科学技术大学和英国卡迪夫大学发表在TPAMI 2021上的论文从配准误差的度量方式以及ICP的迭代更新方式两方面考虑，提出了基于ICP的鲁棒高效刚性配准算法(图1展示了提出的方法与传统ICP注册过程的比较)。其中，所提出的基于固定点迭代加速的思路将传统ICP的收敛速度提高一倍左右，所提出的自适应鲁棒函数调整算法将配准精度提高了约一个数量级。

图1： 提出的方法与ICP方法[1]的配准过程比较，展示了随时间变化的配准状态，以0.5倍速显示配准过程。

2.论文题目
[IEEE TPAMI 2021] Fast and Robust Iterative Closest Point
张举勇（中国科学技术大学），要宇馨（中国科学技术大学），邓柏林（Cardiff University）
论文链接：https://arxiv.org/abs/2007.07627
代码开源：https://github.com/yaoyx689/Fast-Robust-ICP

3.创新点
        (1)提出了自适应调整权值的鲁棒刚性配准模型，其中采用了统计学中的Welsch函数来衡量配准误差，这使得该模型不易受缺失数据以及异常值的影响；

        (2)为了提高该模型的求解速度，将刚性变换矩阵用李代数形式表示，并采用适用于固定点问题的安德森加速方法对算法进行加速，极大地提高了算法的收敛速度。

4.相关工作
        4.1 传统ICP算法 [1]。给定源点云与目标点云，ICP算法首先在源点云与目标点云之间通过查找最近点建立对应关系，然后根据建立的对应关系求解刚性变换矩阵以使得变换之后的源点云与目标点云接近。上述过程交替迭代：

        其中，为旋转矩阵， 为平移向量，, 表示单位阵，为迭代次数。

        4.2 鲁棒ICP算法。由于最近点容易受到缺失数据以及异常值等影响，而距离远的对应点对通常是不可靠的，[2]提出Sparse-ICP方法，采用作为对应点之间距离的度量，即更改Alignment step为：

        该目标函数使得距离远的对应点影响较小，从而提高了配准精度。然而，为了处理目标函数的非凸非线性性，所采用的ADMM求解算法使得该模型的求解速度远低于传统ICP方法。
        4.3提高ICP算法收敛速度。通过将ICP算法中的两步交替迭代步骤合并为一步固定点迭代，[3]提出用安德森加速来提高其收敛速度。为解决安德森加速算法的不稳定，该论文还提出了两种启发式策略。然而，该算法采用欧拉角作为刚性变换的参数化形式来进行安德森加速，而欧拉角存在的万向节锁问题使得源模型和目标模型在配准过程中可能存在歧义角度而减慢收敛速度，另外所提出的启发式策略也存在计算复杂度较高的问题。

5.方法描述
        5.1 自适应的鲁棒距离度量。
采用Welsch函数（如图2）作为对应点之间的距离度量建立优化模型， 即对于Alignment step， 优化

图2：Welsch函数
        由于目标函数的非凸性及非线性性，不易直接求解，故采用Majorization-minimization算法求解该目标函数，首先根据当前迭代值构造该目标函数易于求解的上界函数，使得该上界函数满足在当前迭代值与目标函数值相同，在其他位置均大于目标函数值， 即：

        其中，为二次函数形式。然后求解该二次上界函数，由于其为带权的最小二乘形式，易于通过SVD分解求得其显示解。图3展示了采用MM算法得到新一步迭代值的示意图。

图3： Majorization-minimization算法示意图

        为了适当选取Welsch函数参数值以达到自适应的求解刚性配准问题，考虑到初始位置时源点云和目标点云之间的距离较近的最近点不准确，采用由粗糙到精细的配准过程。将初始的最近点之间的距离中值的倍数作为参数的初始值，并在该参数值下达到收敛后减小值继续优化，直到达到选取的终止值时停止，终止值由源点云和目标点云的密度决定。

        5.2 加速算法收敛。

        考虑到Correspondence step与Alignment step交替求解收敛较慢，且注意到两步结合起来可以视为以为变量的固定点迭代问题，而安德森加速算法对于这类问题可以以很低的计算复杂度高效加速。该加速算法利用当前的迭代值与前m次的历史迭代值通过仿射组合得到加速解，即

        其中为最优仿射系数。因此该论文采用安德森加速来加快收敛，但由于该加速具有不稳定性，由其得到的加速解并不能保证目标函数值是降低的，因此提出的方法采用一种简单的策略使得该加速算法能单调下降，即直接通过判断目标函数值是否降低来决定是否接受加速解，当加速解不能使得目标函数值下降时，则用加速前的解作为当前迭代最优解。迭代求解直到收敛。由于刚性变换空间的李代数为一个向量空间，对加法封闭，且其不存在欧拉角的万向节锁问题，故将刚性变换矩阵采用李代数形式表示作为安德森加速的迭代值。

6.实验结果
        6.1 评价标准。该论文采用源点云经过求得的刚性变换及ground truth变换后的位置差异(RMSE)作为评价标准来衡量实验结果，即

        6.2 合成数据集的比较。图4展示了EPFL statue数据集中构造的Monkeys模型配准结果的比较，提出的点到点的方法Ours (Robust ICP)和点到平面的方法Ours (Robust ICP-l)分别达到了最高及次高的配准精度，对传统ICP方法的加速Ours (Fast ICP)以最快的速度达到了收敛。图5展示了提出的方法对不同异常值的鲁棒性，可以看到除了增加异常值的比例为50%之外(该情况下所有方法均匹配失败)，提出的点到平面的方法Ours (Robust ICP-l)都达到了最高的求解精度，提出的点到点的方法Ours (Robust ICP)也在没有用到法向信息的方法中达到了最高的求解精度。

图4： 对EPFL statue数据集中Monkeys模型的配准结果比较。

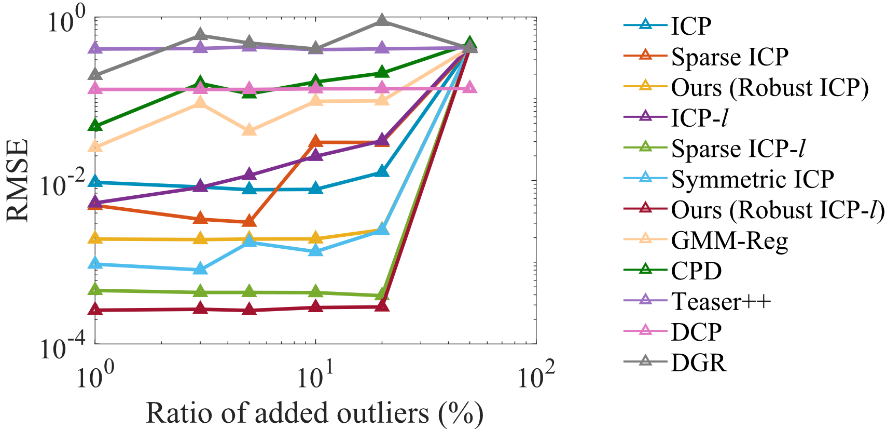
图5：带有不同水平异常值的模型上的配准结果比较。

        6.3真实数据集的比较。该论文也测试了在一些真实数据集上的表现，表1展示了提出的方法与只基于点坐标信息的迭代优化方法在RGB-D SLAM数据集的比较，图6可视化了teddy数据序列中的一个例子，可以看到提出的方法Ours (Robust ICP)达到了最高的配准精度，对传统ICP方法的加速Ours (Fast ICP)以最快的速度达到了收敛。

表1：在RGB-D SLAM数据集上不同方法配准结果的比较，最佳结果被加粗显示。

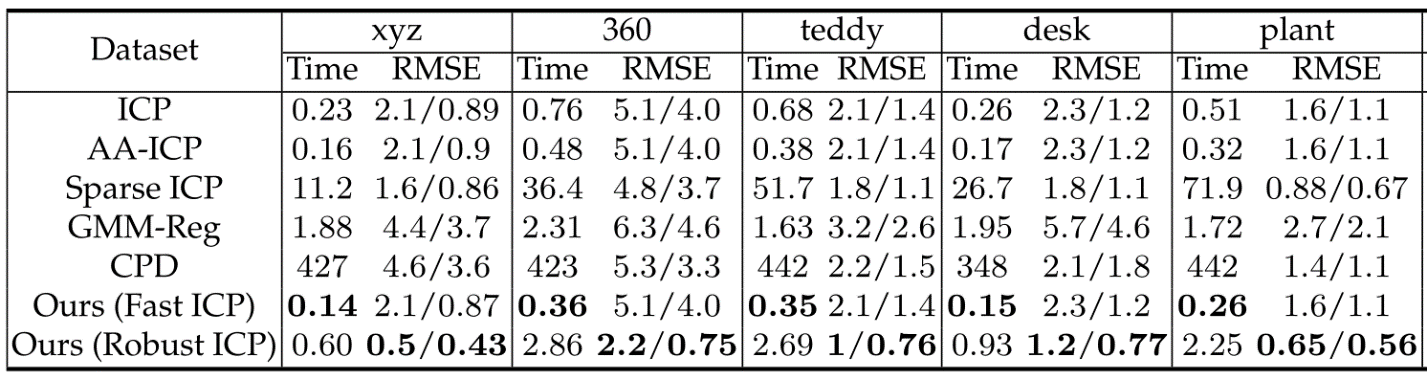
  图 6：teddy数据集上不同方法的配准结果比较， 右下角渲染了配准结果与ground truth逐点之间的误差。

7.参考文献
[1] P. J. Besl and N. D. McKay, “A method for registration of 3-d shapes,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 14, no. 2, pp. 239–256, 1992.
[2] S. Bouaziz, A. Tagliasacchi, and M. Pauly, “Sparse iterative closest point,” Comput. Graph. Forum, vol. 32, no. 5, pp. 113–123, 2013.
[3] A. L. Pavlov, G. V. Ovchinnikov, D. Y. Derbyshev, D. Tsetserukou, and I. V. Oseledets, “AA-ICP: iterative closest point with Anderson acceleration,” in 2018 IEEE International Conference on Robotics and Automation (ICRA), 2018, pp. 1–6