1.论文动机

        近年来，随着激光扫描技术的发展，使得获取物体表面高精度、高密度的点云数据成为可能。由于受物体遮挡以及扫描范围等限制，激光扫描仪无法从单个角度获取物体或场景完整的形状信息。为了获得物体或场景完整的三维点云模型，需要将不同视角下采集获得的点云数据转换到同一坐标系下，由此出现了点云配准问题。根据待配准点云的数目，点云配准可分为双视角点云配准和多视角点云配准问题。通常情况下，多视角点云配准问题难于双视角点云配准问题，且受到的关注较少。为了实现多视角点云的精确配准，我们需要使用全部有效信息计算各帧点云相对于基准坐标系的空间变换关系。然而，许多方法仅仅只利用了部分点云之间的点对信息计算各帧点云的坐标变换关系，从而降低了多视角点云配准结果的精度；另外一些方法盲目地利用点云之间冗余的点对信息计算各帧点云的坐标变换关系，从而降低了多视角点云配准的效率。在确保配准效率的前提下，如何合理地使用不同点云之间的有效消息，精确地计算各帧点云的变换关系是当前多视角点云配准研究领域的难题。今天向大家介绍一篇西安交通大学软件学院视觉计算与机器学习团队发表在IEEE Transaction on Image Processing 2020上的论文，即期望最大化视角下的多视角点云配准方法，该方法在确保配准效率的前提下，可获得令人满意的配准精度。

2.论文题目

[IEEE Transaction on Image Processing 2020] Registration of Multi-View Point Sets Under the Perspective of Expectation-Maximization

祝继华（西安交通大学），郭瑞（西安交通大学），李钟毓（西安交通大学），张婧（中南财经政法大学），庞善民（西安交通大学）

论文链接: https://ieeexplore.ieee.org/abstract/document/9201412

代码开源: https://github.com/Macariaa/EMPMR

3.创新点

        基于期望最大化算法，本文提出了一个名为EMPMR的方法。由于传感器采集的数据不可避免地含有噪声，EMPMR假设每个数据点都分别是由各自的高斯混合模型（Gaussian Mixture Model, GMM）产生的，该数据点在其他点集上的真实对应点视为GMM的质心集合。由于在配准问题中很难找到真实的对应点，EMPMR利用彼此对齐的点集中的最近邻来近似对应点。此外，考虑到局外点的拟合问题，我们在GMM中添加均匀分布控件来增强鲁棒性。在此基础上，本文将多视角配准问题引入最大似然估计框架，并通过期望最大化算法进行优化。该工作的贡献有：

（1）使用概率模型（GMM）对数据进行建模，充分考虑了数据噪声和局外点的拟合。

（2）EMPMR通过建立数据点与真实对应点的关系来定义高斯混合模型中的高斯分量，相比于使用聚类方式，不存在信息丢失问题。并且高斯混合模型中的高斯组件数量是由点云集合的数量自动确定的。因此，配准的准确性和效率之间不存在权衡。

（3）在参数更新时，只需要估计刚性变换和一个协方差。估计参数少，更易获得最优解。

（4）设计实验证实了算法的优越性，并且能高效应用于场景重建和移动机器人SLAM。

4.相关工作

4.1双视角点云配准

        双视角点云配准最流行的方法之一是迭代最近点算法（Iterative Closet Point, ICP）算法[1]，ICP算法依靠最小二乘目标，容易受到噪声、异常值和遮挡的影响。为了提高性能，出现了许多ICP算法的变体。对于不重叠的点集，Chetverikov等提出了裁剪ICP (Trimmed Iterative Closet Point, TrICP)算法[2]，通过引入裁剪比率，有效的选择出两点集中对应的部分，进而利用 ICP 算法对重叠部分进行配准。最近，高斯混合模型（GMM）[3][4][5]被使用到了双视角配准当中，引入概率模型后大大提高了配准的精度。

4.2多视角点云配准

        多视角点云配准通常使用的方法为连续成对配准，这种配准形式的缺点显而易见，即使每对配准都是正确的，但将双视角点云配准串联起来会将误差累积，最终产生不精确的效果。如果还存在不正确的对应，最后的效果会更加糟糕，故而Govindu和Pooja提出了运动平均算法[6]，该算法能够在一组成对配准的基础上，估计全局最优配准顺序。最近，GMM也被用到多视角点云配准当中。Evangelidis等[7]假设点云集合中的每个点都是由同一个GMM生成的，它的质心集合是通过聚类生成。这样在配准过程中便能结合全部点云信息进行配准，避免累计误差的产生。

5.方法描述

5.1 问题定义

        多视角点云配准的目标是计算 帧点云到基准坐标系下的刚性变换 。当扫描仪在对物体或场景进行扫描时，对于物体或场景中的同一位置，每个扫描点集中最多只能获得一个点，因此每个数据点在其他点集中最多只有一个对应点。为了实现多视角点云配准，通常需要在不同的点集之间建立点对应关系。然而，由于噪声或传感器分辨率的影响，所有对应点并不是完全重合的状态。即使是相互配准良好的点集之间，也很难直接建立精确的点对应关系。为此，我们将最近邻关系近似为真实对应关系。考虑到数据噪声，可以假设点集中的每个数据点分别是由一个高斯分布生成的，该数据点的对应点为高斯分布的质心。为了进一步从所有其他点集探索更多可用的信息，我们假设每个数据点分别是由各自的GMM生成的，每个数据点在其他点集中的对应点集合被视为各自GMM的质心集合。图1为算法的示意图。

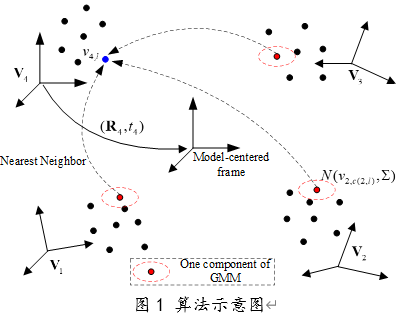
        设V=为M帧点云集合，其中，为第i帧点云中的数据点数量。表示点在除自身之外的其他点集中搜索到的最近邻集合。此外，我们对所有的GMM组件使用相等的协方差和相等的隶属概率。在此假设下，数据点的联合概率公式如下：

        上式中M’=M-1，与R分别表示第i帧点云到基准坐标系下的旋转矩阵和平移向量。为了简单起见，我们将施加在上的空间变换定义为公式。考虑到数据中含有噪声和异常值，需要在概率公式中加入额外的均匀分布来拟合。

5.2 期望最大化算法求解最优参数   

        为了得到参数集合最优更新的封闭解，本节将利用期望最大化算法进行求解。使用期望最大化框架求解，需要完整的数据集合。因此，需要定义一组隐变量 表示点在第j帧点云集合中的最近邻为。给定所有点云集合V，可以通过最大化对数似然函数的期望来估计模型参数，如下所示：

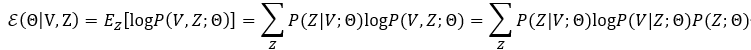
        当我们对所有GMM组件使用相同的隶属概率时，为常数项。因此简化为：

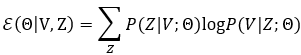
        上式中描述的问题可以通过期望最大化算法进行优化，该方法可以最大化似然函数来估计所有的刚性变换。该方法被称为最大化期望下的多视角点云配准算法(Expectation-Maximization Perspective for Multi-view Registration, EMPMR)，EMPMR中的每次迭代都包含E-step和M-step。

5.2.1 E-step

1) E-Corresponding-Step: 对于第i帧点云集合中的一个数据点，我们需要找到它在其他点集中最近邻。每个数据点可以通过下式搜索到M’个最近邻，作为各自GMM的质心集合

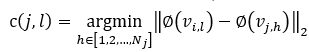
2) E-Probability-Step: 给定质心集合和协方差Σ，数据点的后验概率计算如下:

其中

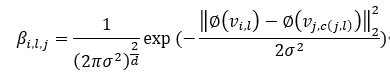
5.2.2 M-step

        在M-Step中，通过最大化，对完整模型参数进行更新。虽然很难同时估计这些模型参数，但它们的估计可以顺序地、独立地进行。

6.实验结果

        EMPMR在几个公开数据集上进行了测试，包括六个对象数据集和环境数据集。并且为了说明其性能，EMPMR与五个最先进的方法进行对比：基于TrICP的运动平均法[6]、多视角点云联合配准方法[7]，基于TrICP的低秩和稀疏分解方法[8]，基于Student’s T混合模型的多视角点云配准方法[9]和基于K-means的方法[10]，缩写分别为MATrICP， JRMPC，TMM，LRS和K-means。实验结果的对比形式为相对于ground truth的配准误差，其中包括旋转误差和平移误差。表1为本次实验所使用对象数据集的基本信息。

        表2中展示了所有方法在六个数据集上的运行结果，其中4个数据集选自Stanford 3D扫描存储库[11]，另外两个数据集由Torsello等[12]扫描得出。给定每个数据集初值的情况下，实验结果表明，与其他五种方法对比，EMPMR在绝大多数条件下表现出了更好的性能。

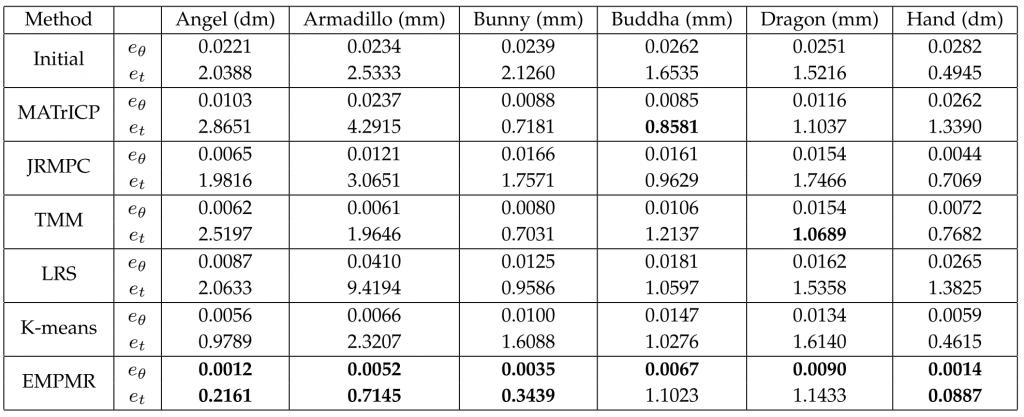
        图2还展示了每种配准算法应用在环境数据集上的结果，在此数据集中，所有扫描对都包含较高的重叠百分比。在使用多视角点云配准算法进行场景重建时，算法只处理距离信息，并利用颜色信息辅助最终的评估。可以看出EMPMR具有对RGB-D数据进行多视角配准的潜力，可有效的应用于场景重建。

        更多应用示例细节，如将算法应用于机器人SLAM定位中，以及对于算法性能的全方位展示和比较，详细请见论文原文。

7.参考文献

[1] Besl P J, McKay N D. Method for registration of 3-D shapes[C]//Sensor fusion IV: control paradigms and data structures. International Society for Optics and Photonics, 1992, 1611: 586-606.

[2] Chetverikov D, Stepanov D, Krsek P. Robust Euclidean alignment of 3D point sets: the trimmed iterative closest point algorithm[J]. Image and vision computing, 2005, 23(3): 299-309.

[3] Myronenko A, Song X. Point set registration: Coherent point drift[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(12): 2262-2275.

[4] Jian B, Vemuri B C. Robust point set registration using gaussian mixture models[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 33(8): 1633-1645.

[5] Gao W, Tedrake R. Filterreg: Robust and efficient probabilistic point-set registration using gaussian filter and twist parameterization[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 11095-11104.

[6] Govindu V M, Pooja A. On averaging multiview relations for 3D scan registration[J]. IEEE Transactions on Image Processing, 2013, 23(3): 1289-1302.

[7] Evangelidis G D, Horaud R. Joint alignment of multiple point sets with batch and incremental expectation-maximization[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 40(6): 1397-1410.

[8] Arrigoni F, Rossi B, Fragneto P, et al. Robust synchronization in SO (3) and SE (3) via low-rank and sparse matrix decomposition[J]. Computer Vision and Image Understanding, 2018, 174: 95-113.

[9] Ravikumar N, Gooya A, Çimen S, et al. Group-wise similarity registration of point sets using Student’s t-mixture model for statistical shape models[J]. Medical image analysis, 2018, 44: 156-176.

[10] Zhu J, Jiang Z, Evangelidis G D, et al. Efficient registration of multi-view point sets by K-means clustering[J]. Information Sciences, 2019, 488: 205-218.

[11] B. C. M. Levoy, J. Gerth, and K. Pull. (2005). The Stanford 3D Scanning Repository. [Online]. Available: http://www-graphics.stanford.edu/data/3dscanrep

[12] Torsello A, Rodola E, Albarelli A. Multiview registration via graph diffusion of dual quaternions[C]//CVPR 2011. IEEE, 2011: 2441-2448.